En ampliación a la publicación: Temas Místicos Rosacruces: La Pineal o Epífisis (séptima rosa)
publicamos este envío, que agradecemos.
La pineal o epífisis es la que se relaciona con lo que los orientales llaman el ojo de Horus.
Quizás amerite ampliar esto y que sea de vuestro agrado:
“la glándula Pineal hay que tener en cuenta, que forma parte de un sistema mayor y que enriquece sus funciones y les da la fuerza y asentamiento precisos. En este sistema se incluyen las glándulas:Timo, Pituitaria, Pineal y el Hipotálamo, como pilar y sustento de todo el conjunto. Pero también, necesitamos un anclaje para todo este sistema de activación frecuencial que nos permita estar estables, y que nuestro organismo no sienta alteraciones ante este torrente de energía, por lo que también tendremos que activar y trabajar con las glándulas suprarrenale, que son las que están en sintonía con el chakra Raíz, encargado de este anclaje. De aquí, la energía descenderá hasta la tierra siguiendo el canal de conexión con ella.
Las glándulas, en general, son centros del control de nuestro organismo, desde el punto de vista físico, pero también tienen una implicación y actividad asociada a nuestro sistema anatómico energético.
Las Glándulas Endocrinas son los puntos de conexión del cuerpo físico con el energético a través de los chakras. Estos dos puntos, glándula y chakra, son los enlaces que hacen que la energía entre en el cuerpo y lo reestructure, así como la red electromagnética que lo recubre. Así, las glándulas, se consideran portales o puentes a los distintos planos o niveles de conciencia. Dependiendo de la glándula podremos conectar con uno u otro plano, en resonancia con el tipo de energía que mueven y sus funciones orgánicas. Si seguimos el orden de planos desde el más próximo a 3D, al más alejado, el orden glandular sería el siguiente:
Adrenales o Suprarrenales, Gónadas, Páncreas, Timo, Tiroides, Pituitaria o Hipófisis y Pineal o Epífisis. Sobre ellas está el Hipotálamo como filtro de todo, como puente entre el sistema nervioso y el hormonal.
Otro aspecto muy importante para la activación del Ojo de Horus, es que no es una activación mecánica, que con tocar energéticamente o poniendo unos símbolos, es suficiente, es más que todo eso. Para una verdadera, armoniosa y duradera activación del Ojo de la Mente, es preciso un constante trabajo interno, hay que ser responsables de lo que se quiere hacer y de la propia evolución, entendiendo que si no se produce este trabajo, no se dará una transformación de base, necesaria y fundamental para que la glándula pineal y todo el sistema cambie su frecuencia y se active. Es preciso que haya una total conexión con el ser interno y, por tanto, que se tenga bien identificado todo lo que desde la sombra actúa sobre nuestra psique y nos trampea el camino. Pero, ¿qué es esto que está en la sombra? Nuestro propio inconsciente, lo que tenemos ahí guardado y tapado para que parezca que no existe, que no está.
Por tanto, cuando realizamos este trabajo de reconocimiento interno y de depuración de todo aquello que no vibre en la frecuencia adecuada, tenemos que entender que lo más importante es conseguir unificarnos como un ser y, para esto, mente y corazón tienen que ir de la mano. Esto dos puntos son las dos piedras angulares de nuestro ser y, por tanto, no pueden ir cada una por un lado, es fundamental que caminen de la mano y se ayuden a realizar los cambios.
“la glándula Pineal hay que tener en cuenta, que forma parte de un sistema mayor y que enriquece sus funciones y les da la fuerza y asentamiento precisos. En este sistema se incluyen las glándulas:Timo, Pituitaria, Pineal y el Hipotálamo, como pilar y sustento de todo el conjunto. Pero también, necesitamos un anclaje para todo este sistema de activación frecuencial que nos permita estar estables, y que nuestro organismo no sienta alteraciones ante este torrente de energía, por lo que también tendremos que activar y trabajar con las glándulas suprarrenale, que son las que están en sintonía con el chakra Raíz, encargado de este anclaje. De aquí, la energía descenderá hasta la tierra siguiendo el canal de conexión con ella.
Las glándulas, en general, son centros del control de nuestro organismo, desde el punto de vista físico, pero también tienen una implicación y actividad asociada a nuestro sistema anatómico energético.
Las Glándulas Endocrinas son los puntos de conexión del cuerpo físico con el energético a través de los chakras. Estos dos puntos, glándula y chakra, son los enlaces que hacen que la energía entre en el cuerpo y lo reestructure, así como la red electromagnética que lo recubre. Así, las glándulas, se consideran portales o puentes a los distintos planos o niveles de conciencia. Dependiendo de la glándula podremos conectar con uno u otro plano, en resonancia con el tipo de energía que mueven y sus funciones orgánicas. Si seguimos el orden de planos desde el más próximo a 3D, al más alejado, el orden glandular sería el siguiente:
Adrenales o Suprarrenales, Gónadas, Páncreas, Timo, Tiroides, Pituitaria o Hipófisis y Pineal o Epífisis. Sobre ellas está el Hipotálamo como filtro de todo, como puente entre el sistema nervioso y el hormonal.
Otro aspecto muy importante para la activación del Ojo de Horus, es que no es una activación mecánica, que con tocar energéticamente o poniendo unos símbolos, es suficiente, es más que todo eso. Para una verdadera, armoniosa y duradera activación del Ojo de la Mente, es preciso un constante trabajo interno, hay que ser responsables de lo que se quiere hacer y de la propia evolución, entendiendo que si no se produce este trabajo, no se dará una transformación de base, necesaria y fundamental para que la glándula pineal y todo el sistema cambie su frecuencia y se active. Es preciso que haya una total conexión con el ser interno y, por tanto, que se tenga bien identificado todo lo que desde la sombra actúa sobre nuestra psique y nos trampea el camino. Pero, ¿qué es esto que está en la sombra? Nuestro propio inconsciente, lo que tenemos ahí guardado y tapado para que parezca que no existe, que no está.
Por tanto, cuando realizamos este trabajo de reconocimiento interno y de depuración de todo aquello que no vibre en la frecuencia adecuada, tenemos que entender que lo más importante es conseguir unificarnos como un ser y, para esto, mente y corazón tienen que ir de la mano. Esto dos puntos son las dos piedras angulares de nuestro ser y, por tanto, no pueden ir cada una por un lado, es fundamental que caminen de la mano y se ayuden a realizar los cambios.
El humano en realidad tiene dos cerebros, el intelectual y el emotivo; el que piensa y el que ama. Pero solo cuando lo unificamos, podemos decir que pensamos con el corazón y sentimos con el cerebro y no es ninguna tontería o juego de palabras, porque la realidad es ésta. A esto se le llama la unificación mente-corazón y así y solo así podremos caminar unificados.
Para conectar y activar este Ojo de Horus o el Ojo de la Mente, se realizan una serie de iniciaciones, mediante meditaciones y visualizaciones guiadas, que lo posibiliten. No son ejercicios para abrir la clarividencia, sino para despertar la visión interna, la visión espiritual que nos indicará lo que en realidad son las cosas. Nos mantendrá despiertos y alertas independientemente de nuestro estado de vigilia o de sueño.
Igualmente, la glándula pineal, tendrá una mejor actividad y no solo para nuestros dones o despertar a los otros niveles de conciencia, sino también a su funcionalidad física.
Así, sucederá que podremos conectar con nuestra Sabiduría ancestral, a través de mi auténtico Yo, por tanto, podremos decir: YO SE, PORQUE YO SOY.
Para conectar y activar este Ojo de Horus o el Ojo de la Mente, se realizan una serie de iniciaciones, mediante meditaciones y visualizaciones guiadas, que lo posibiliten. No son ejercicios para abrir la clarividencia, sino para despertar la visión interna, la visión espiritual que nos indicará lo que en realidad son las cosas. Nos mantendrá despiertos y alertas independientemente de nuestro estado de vigilia o de sueño.
Igualmente, la glándula pineal, tendrá una mejor actividad y no solo para nuestros dones o despertar a los otros niveles de conciencia, sino también a su funcionalidad física.
Así, sucederá que podremos conectar con nuestra Sabiduría ancestral, a través de mi auténtico Yo, por tanto, podremos decir: YO SE, PORQUE YO SOY.
Ing. Jose Mejia
Agradecemos a Ing. José Mejia, por este aporte
*






 y
y  , y la medida de la
, y la medida de la  , se establece que:
, se establece que:
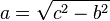

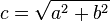
















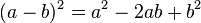
 .
.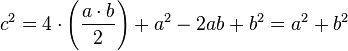

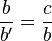


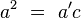
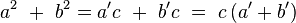
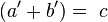 , por lo que finalmente resulta:
, por lo que finalmente resulta:


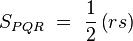
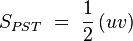
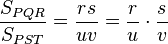
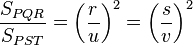
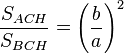
 (I)
(I)
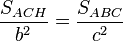
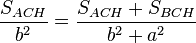 , así que:
, así que:
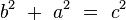

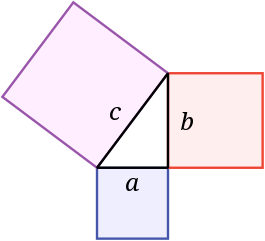
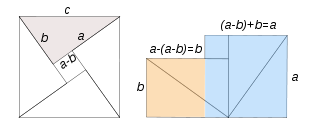
 ) equivale a la de los cuadrados amarillo y azul (
) equivale a la de los cuadrados amarillo y azul ( ), habiéndose demostrado el teorema de Pitágoras.
), habiéndose demostrado el teorema de Pitágoras.



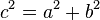



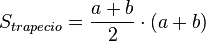


 y simplificando...
y simplificando...
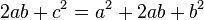
 a ambos miembros, finalmente nos da:
a ambos miembros, finalmente nos da: